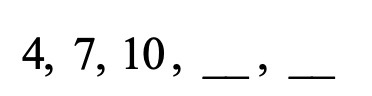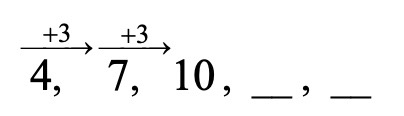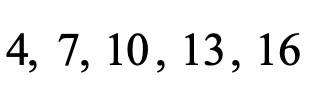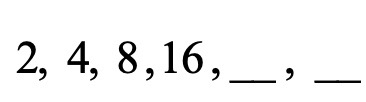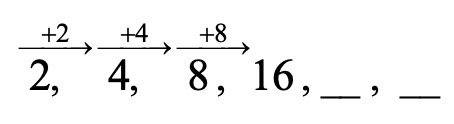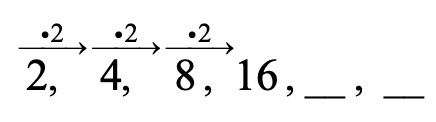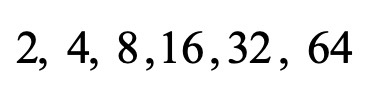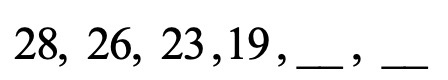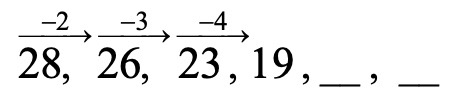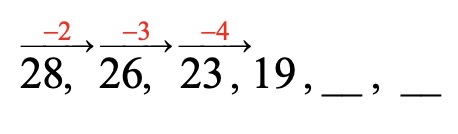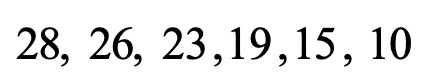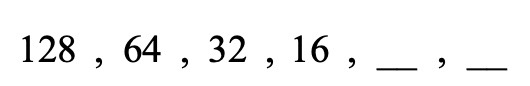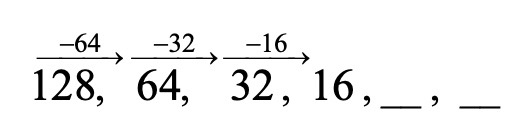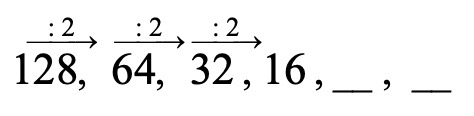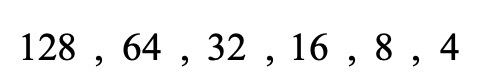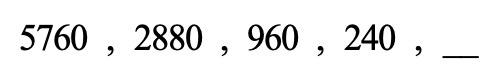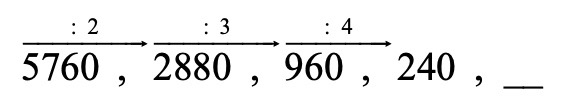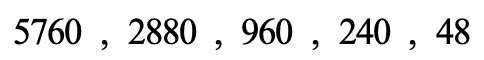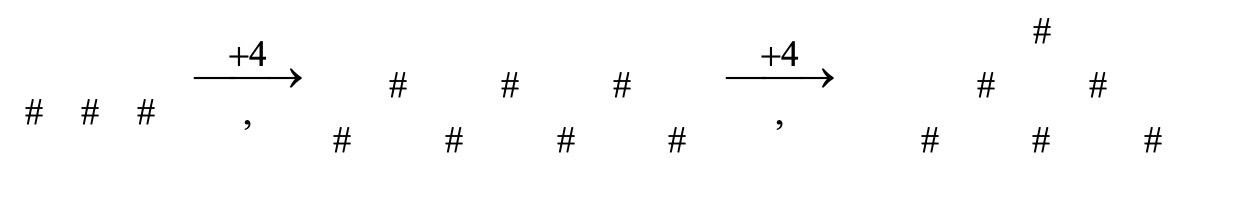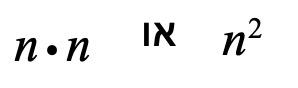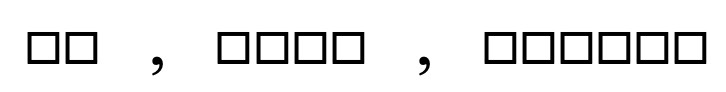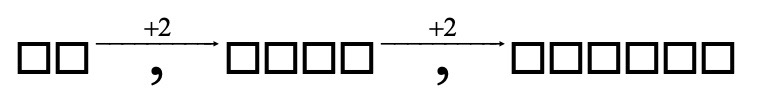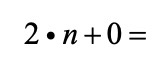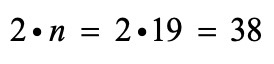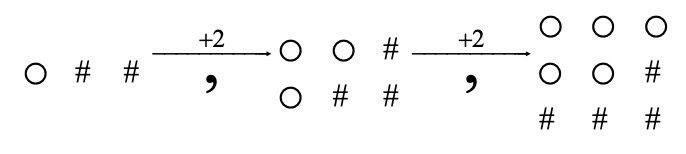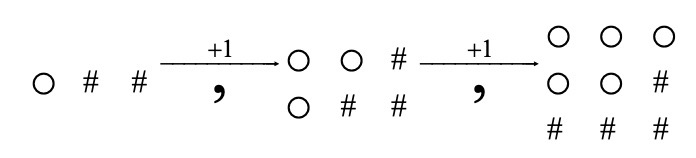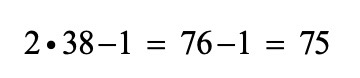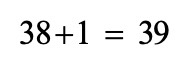עמוד הבית » דפי עבודה במתמטיקה » מתמטיקה לכיתה ז » חוקיות לכיתה ז׳
חוקיות לכיתה ז׳
מציאת חוקיות לסדרות מספרים
⇐ בתרגילי חוקיות נבדוק תמיד תחילה האם ישנה חוקיות בפעולות החיבור והחיסור – האם איברי הסדרה גדלים או קטנים במספר מסוים.
⇐ במידה ואין מספר כזה, נבדוק את פעולות הכפל והחילוק – האם איברי הסדרה גדלים או קטנים פי מספר מסוים.
⇐ ומה אם ארבעת פעולות החשבון שבדקנו אינן מתאימות לתיאור החוקיות בסדרה ?
נבצע את בדיקת החוקיות הרגילה (נבדוק בכמה גדול או קטן כל איבר) ונבדוק האם ההפרש בין המספרים גדל או קטן בחוקיות מסוימת.
דוגמאות
דוגמא 1: חוקיות בפעולות חיבור וחיסור
נתבונן בדוגמא הבאה :
∗ ננסה למצוא את החוקיות בסדרה ולהשלים את שני האיברים הנותרים.
∗ כאשר נחפש חוקיות לסדרה, תמיד נבדוק תחילה האם הסדרה גדלה או קטנה במספר קבוע.
ניתן לראות שישנה קפיצה קבועה ב-3 בכל מעבר מאיבר אחד לאיבר הבא אחריו.
לכן החוקיות היא שאיברי הסדרה גדלים בכל קפיצה ב-3.
∗ נשלים :
נתבונן בדוגמא הבאה:
∗ כמו בתרגיל הקודם, נבדוק תחילה האם הסדרה גדלה או קטנה במספר קבוע:
אנחנו רואים כעת שהקפיצה איננה קבועה.
∗ כעת נבדוק האם איברים הסדרה גדלים או קטנים פי מספר מסוים:
מצאנו את החוקיות ! החוקיות היא שאיברי הסדרה גדלים פי 2.
∗ נשלים :
נתבונן בדוגמא הבאה :
∗ נבצע את הבדיקה שאנו רגילים לבצע – נסמן תחילה בכמה כל איבר קטן או גדל :
ניתן לראות שאין מספר קבוע שבו איברי הסדרה גדלים או קטנים.
∗ כאשר נבדוק את פעולות הכפל והחילוק נראה שגם הן אינן מתאימות – המספר 28 בכלל לא מתחלק ב-26.
∗ נשים לב להפרש הסדרה – הקפיצה בין איבר לאיבר :
ההפרש גדל ב-1 בכל קפיצה !
לכן חוקיות הסדרה היא שהפרש הסדרה גדל בכל מעבר מאיבר לאיבר ב-1.
∗ נשלים :
מציאת חוקיות לסדרות תרגילים

⇐ נבדוק את הטור הימני בנפרד ואת הטור השמאלי בנפרד – האם איברי הסדרה גדלים או קטנים במספר מסוים :
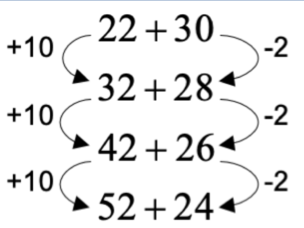
⇐ מצאנו כי האיברים בטור השמאלי גדלים ב-10 ואילו האיברים בטור הימני קטנים ב-2.
⇐ כעת, נשלים את איברי הסדרה החסרים:

תרגול
תרגיל 1
נתונה הסדרה הבאה:
א. מהי חוקיות הסדרה ?
ב. השלימו את איברי הסדרה.
ג. מה יהיה האיבר במקום ה-7 בסדרה ?
נבדוק האם המספרים גדלים או קטנים במספר מסוים:
אין מספר כזה.
נבדוק כעת האם איברי הסדרה גדלים או קטנים פי מספר מסוים :
מצאנו את החוקיות !
החוקיות היא שכל איבר קטן פי 2 מהאיבר שקדם לו.
נשתמש בחוקיות כדי להשלים את האיברים החסרים:
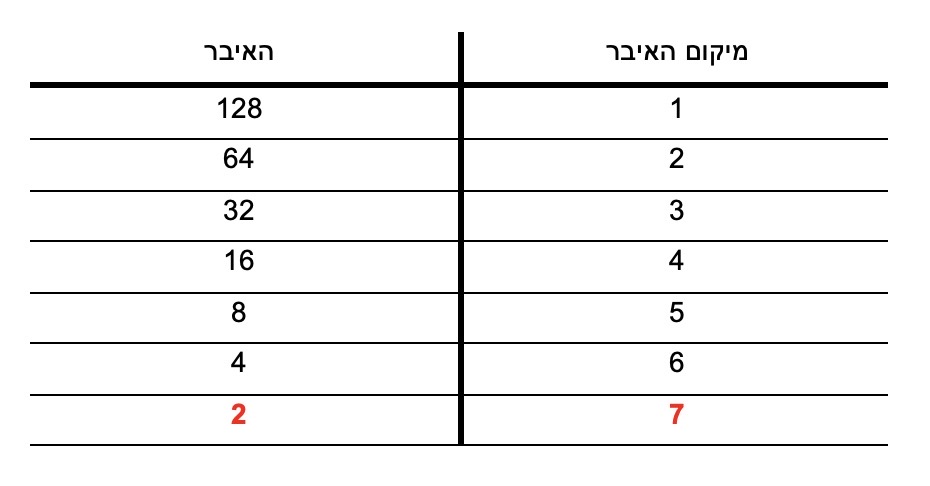
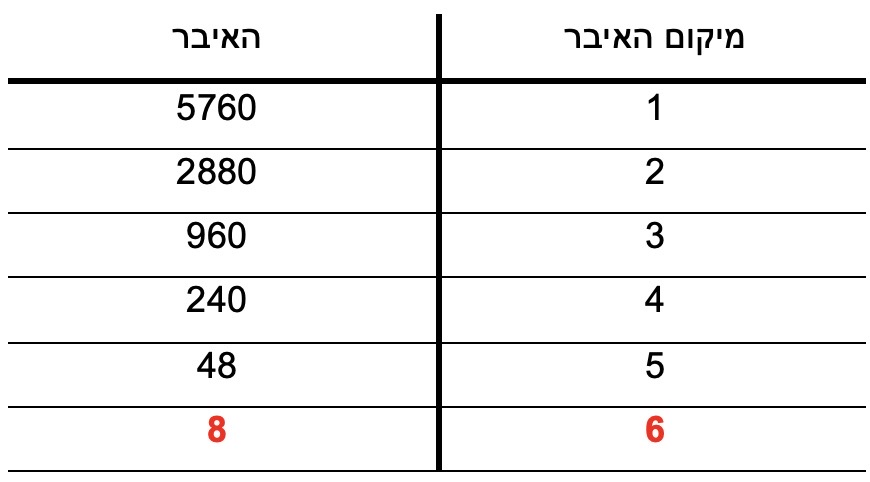
נשתמש בטבלה כדי לרכז את הנתונים :
האיבר במיקום ה-7 הוא 2.
תרגיל 2
נתונה הסדרה הבאה:
א. מהי חוקיות הסדרה ?
ב. השלימו את האיבר החסר בסדרה.
ג. מה יהיה האיבר במקום ה-6 בסדרה ?
מספרי הסדרה לא גדלים או קטנים במספר מסוים.
מספרי הסדרה גם לא גדלים או קטנים פי מספר מסוים.
לכן, נבדוק האם ישנה חוקיות בהפרש בין המספרים בסדרה:
מצאנו!
חוקיות הסדרה היא שהמספר בו מחלקים כל איבר גדל ב-1.
נשתמש בחוקיות כדי להשלים את האיברים החסרים:
נשתמש בטבלה כדי לרכז את הנתונים :
האיבר במקום ה-6 הוא 8.
תרגיל 3
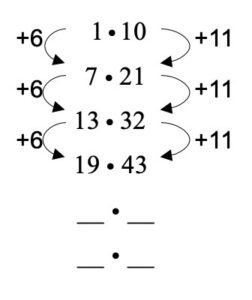
נתונה סדרת התרגילים הבאה :
א. מהי חוקיות הסדרה ?
ב. השלימו את איברי הסדרה.
ג. מה יהיה האיבר במקום ה-8 בסדרה ?
נסתכל על הטור הימני והטור השמאלי בנפרד.
ראשית נבדוק האם האיברים גדלים או קטנים במספר מסוים :
מצאנו את החוקיות ! החוקיות היא שבטור הימני האיברים גדלים ב-2, ובטור השמאלי האיברים קטנים ב-10.
נשלים את איברי הסדרה לפי החוקיות שמצאנו :
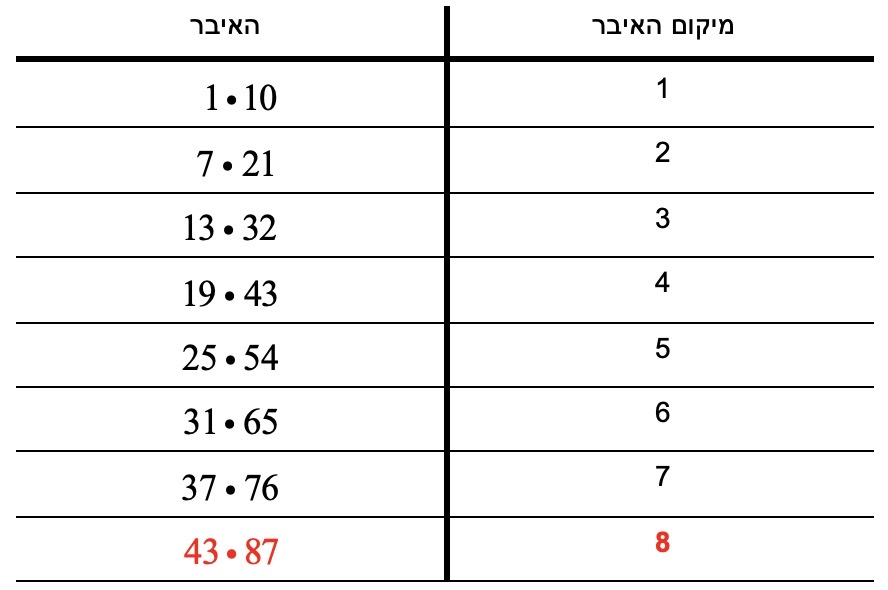
נרכז את איברי הסדרה בטבלה :
האיבר במקום השמיני הוא: 87 • 43
בניית ביטוי אלגברי לחוקיות סדרה
בחלק זה נדגים כיצד לבנות ביטוי אלגברי לחוקיות עבור שני סוגי סדרות:
בניית ביטוי אלגברי לסדרות קבועות
נתבונן בסדרת העיגולים הבאה :
א. כמה עיגולים יהיו באיבר הרביעי והחמישי ?
נבצע את הבדיקה שביצענו עד כה בתרגילי חוקיות – נבדוק האם הסדרה גדלה או קטנה במספר מסוים:
ניתן לראות שבכל איבר נוספים 2 עיגולים.
לכן באיבר הרביעי יהיו 9 עיגולים, ובאיבר החמישי 11 עיגולים.
ב. באיזה איבר יהיו 21 עיגולים ?
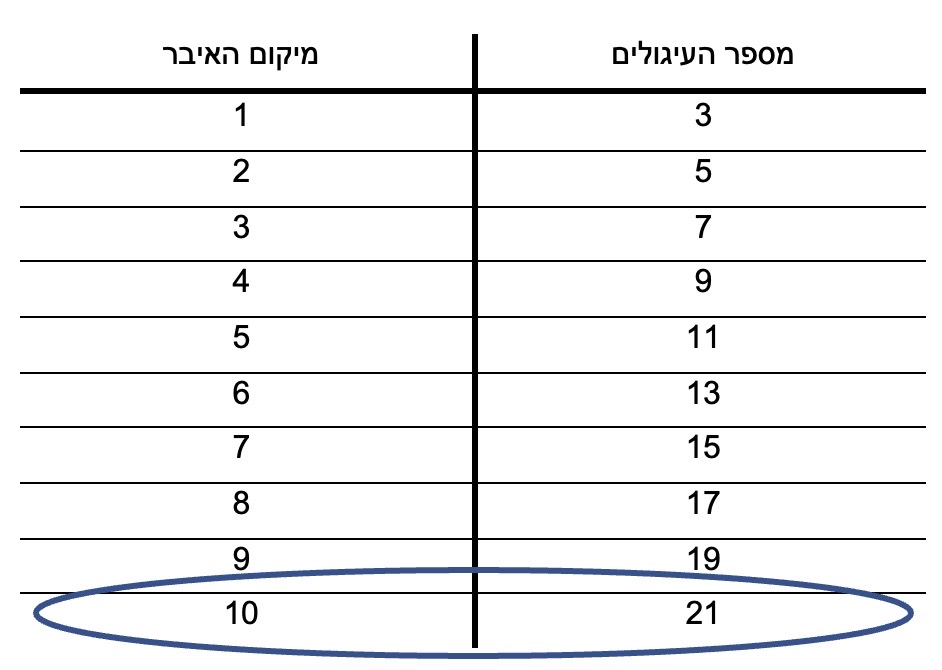
נרכז את איברי הסדרה בטבלה ונשלים עד שנגיע ל-21 עיגולים :
באיבר העשירי יהיו 21 עיגולים !
ג. בטאו באמצעות n את חוקיות הסדרה (בניית ביטוי אלגברי)
כעת נלמד איך לבטא באמצעות n את חוקיות הסדרה – נלמד לבנות ביטוי אלגברי.
n מייצג את מיקום האיבר.
למשל, באיבר הראשון – n=1 , באיבר השני n=2 , באיבר השלישי n=3 וכן הלאה.
נסתכל שוב על הסדרה :
⇐ נתחיל מהקפיצה – מוסיפים 2 לכל איבר.
לכן בבניית הביטוי האלגברי נתחיל ב- 2n.
⇐ כעת נבדוק כמה צריך להוסיף או להחסיר ל-2 (הקפיצה שלנו) על מנת להגיע לכמות הכדורים באיבר הראשון.
באיבר הראשון ישנם 3 כדורים, לכן נצטרך להוסיף לביטוי שבנינו עד כה את המספר 1 : 2n + 1 .
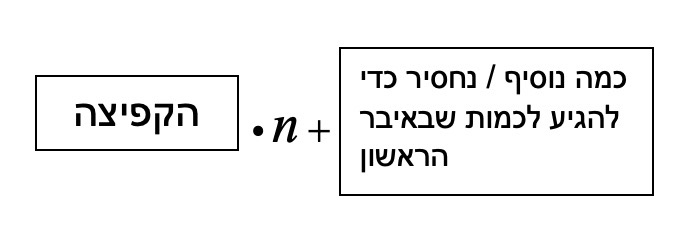
⇐ לסיכום, בניית הביטוי האלגברי עבור חוקיות הסדרה תיראה כך :
נתבונן בדוגמה נוספת וננסה לבנות עבור ביטוי אלגברי שיבטא את חוקיות הסדרה :
ניתן לראות כי מוסיפים 4 לכל איבר – הקפיצה בסדרה היא 4.
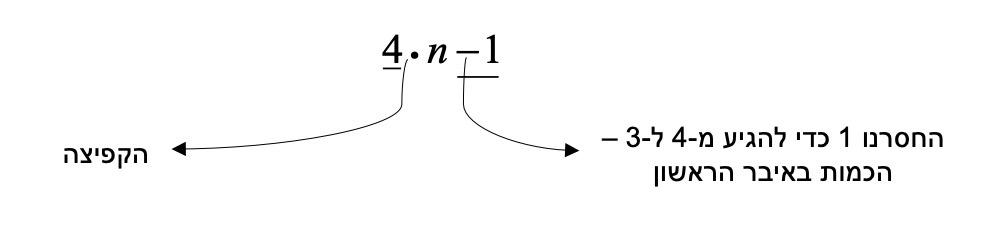
כעת נשאל את עצמנו – כמה צריך להוסיף/להחסיר מ-4 על מנת להגיע ל-3 ? ( 3 הוא מספר המשולשים באיבר הראשון ).
התשובה היא שעלינו להחסיר 1, ולכן הביטוי האלגברי המתאר את חוקיות הסדרה הוא :
בניית ביטוי אלגברי לסדרות לא קבועות (סדרת חזקות)
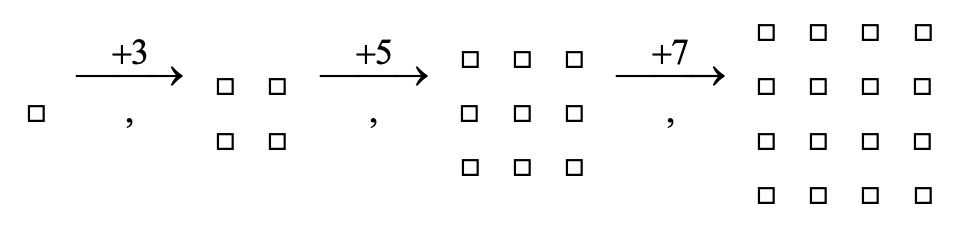
נתבונן בסדרה הבאה :
נבדוק את הקפיצות מאיבר לאיבר כפי שאנחנו רגילים :
נשים לב שהקפיצה איננה קבועה.
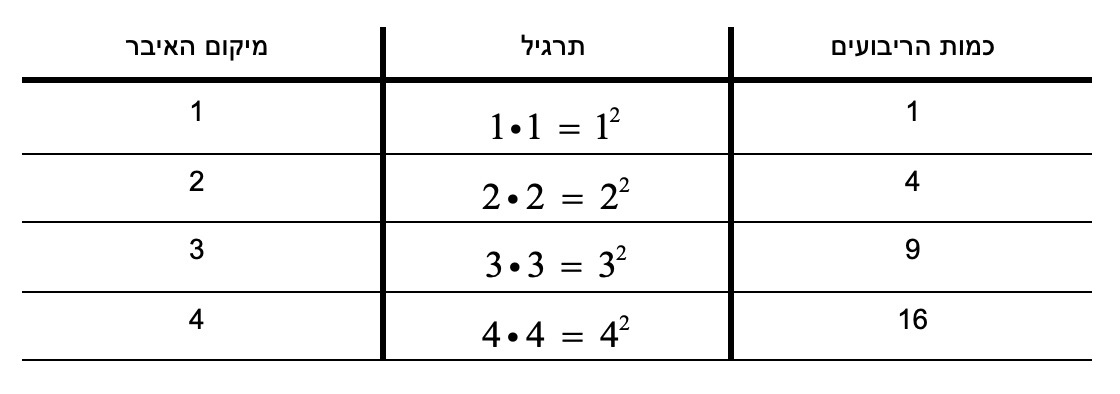
סדרה זו היא סדרת חזקות – כדי לחשב כמה ריבועים יהיו בכל איבר נעלה את מקום האיבר בחזקת 2.
לכן הביטוי האלגברי שמבטא את חוקיות הסדרה הוא בעצם מיקום האיבר כפול עצמו, או במילים אחרות מיקום האיבר בחזקת 2 :
תרגול
תרגיל 1
נתונים 3 האיברים הראשונים בסדרת המרובעים הבאה :
א. בנו ביטוי אלגברי המייצג את מספר המשולשים בכל איבר.
ב. כמה איברים יהיו באיבר ה-19 ?
ראשית נבין את החוקיות :
החוקיות היא שכל איבר גדל ב-2.
כעת נבנה את הביטוי האלגברי, כאשר הקפיצה היא 2, ולא צריך להוסיף או להחסיר כדי להגיע למספר הריבועים באיבר הראשון.
נבנה את הביטוי :
נבדוק את 3 האיברים הראשונים כדי לוודא שהביטוי נכון :
באיבר הראשון באיבר הראשון 2 ריבועים. הביטוי מתאים.
באיבר השני באיבר השני יש 4 ריבועים. הביטוי מתאים.
באיבר השלישי באיבר השלישי יש 6 ריבועים. הביטוי מתאים.
נשתמש בביטוי שמצאנו ונחליף את n ב-19:
באיבר ה-19 ישנם 38 משולשים.
תרגיל 2
נתונים 3 האיברים הראשונים בסדרת הצורות הבאה :
א. בנו ביטוי אלגברי המייצג את מספר העיגולים בסדרה.
ב. בנו ביטוי אלגברי המייצג את מספר המשולשים בסדרה.
ג. כמה עיגולים ומשולשים יהיו באיבר ה-38 ?
מולנו סדרה המורכבת מ-2 צורות – עיגולים ומשולשים.
נקפיד להסתכל על כל צורה בנפרד, בדיוק כמו שעשינו בסדרות תרגילים.
נבין את החוקיות של העיגולים לחוד ושל המשולשים לחוד :
נסתכל רק על העיגולים :
החוקיות היא שמספר העיגולים גדל ב-2 בכל איבר.
באיבר הראשון ישנו עיגול אחד ולכן כדי להגיע לאיבר הראשון צריך להחסיר 1.
נבנה את הביטוי האלגברי : 2n – 1
כעת נסתכל רק על המשולשים :
החוקיות היא שמספר המשולשים גדל ב-1 בכל איבר.
הקפיצה של המשולשים היא 1. באיבר הראשון ישנם 2 משולשים ולכן כדי להגיע לאיבר הראשון צריך להוסיף 1.
נבנה את הביטוי : n + 1
נסתכל על הביטוי המייצג את מספר העיגולים ונחליף את n ב-38 :
כעת נסתכל על הביטוי המייצג את מספר המשולשים ונחליף את n ב-38 :
באיבר ה-38 ישנם 75 עיגולים ו-39 משולשים.
דפי תרגול במספרים מכוונים, חוקיות לכיתה ז'
מוזמנים לבקר בעמוד מתמטיקה לכיתה ז' – בו ניתן לצפות במגוון דפי עבודה ומבחנים במתמטיקה לכיתה ז׳